While I was scouring the reaches of the internet in search of an internship, I came across this lab at IISc working in a peculiar field titled Mathematical Oncology. As expected, I was perplexed and my curiosity had taken complete control. Consequently, I wrote to the PI, and to my surprise, my application was instantly accepted, so fast that I hadn’t had the chance to properly understand what mathematical oncology was.
We all must have come across the concept of mathematical modelling some time during the course of our undergraduate experience. There are simple models like Newton’s classical description of mechanics, and there are models like Schrödinger’s quantum theory which take on unparalleled complexities. Regardless, these mathematical descriptions can replicate the dynamics of the real-life systems they model to great accuracies. But the thought of creating models for cancer, which is a biological phenomenon, was completely alien to me. Biology has an infinite number of variables, exceptions and interactions; how could we possibly capture all of these?
It turns out, it is very much possible, and mathematical models have been constructed in almost every field, from neuroscience to pharmacology. Most of biology is extremely dependent on living model organisms, such as mice and HeLa cells. These model organisms are used to understand ubiquitous phenomena, and the knowledge gained from them is applied to real-world problems such as diseases in humans. For example, if we wanted to study how a mouse reacts to a certain disease, we would introduce the mouse to said disease and observe its reaction. Similarly, when we use a mathematical model, we tinker with the variables to replicate an infection and observe the various outputs of the mathematical relations to infer the model’s reaction. There are advantages and disadvantages to both types of approaches, and each has a unique application. Discussing these applications would require an entirely new article, therefore I will shift the narrative to the work I did in the internship I mentioned initially.
Cancer is quite possibly the most insidious disease yet, as it strikes without warning and it is often too late to save the patient by the time its presence has been detected. It is no surprise that cancer research is the most funded field in pathology and the U.S. went as far as to declare a ‘war on cancer’ in the early 70s. Despite these ongoing efforts, therapeutics aren’t very effective; lung cancer has a survival rate of only 16.2% (over a period of 5 years). Survival chances drop drastically when the cancer spreads to other parts of the body through a phenomenon called metastasis, which is responsible for more than 90% of cancer deaths. Let me briefly explain the bare-bones of metastasis.
When a cancer is formed, it is primarily composed of epithelial cells, which are immobile cells that stick to the surfaces of tissue. For the cancer to spread, the cells must undergo a metamorphosis and gain the characteristics of a mesenchymal cell, which is a mobile cell that does not adhere to surfaces. These troops of mesenchymal cells then spread through the body by entering the bloodstream, after which they exit and arrive at locations where they need to settle and form colonies. For this, they must undergo another metamorphosis and re-attain epithelial characteristics so that they can stick to the tissue and form a new colony. The scientific term for this metamorphosis between cell types (or phenotypes, to be more accurate) is called phenotypic plasticity. This phenomenon was the main focus of my research.
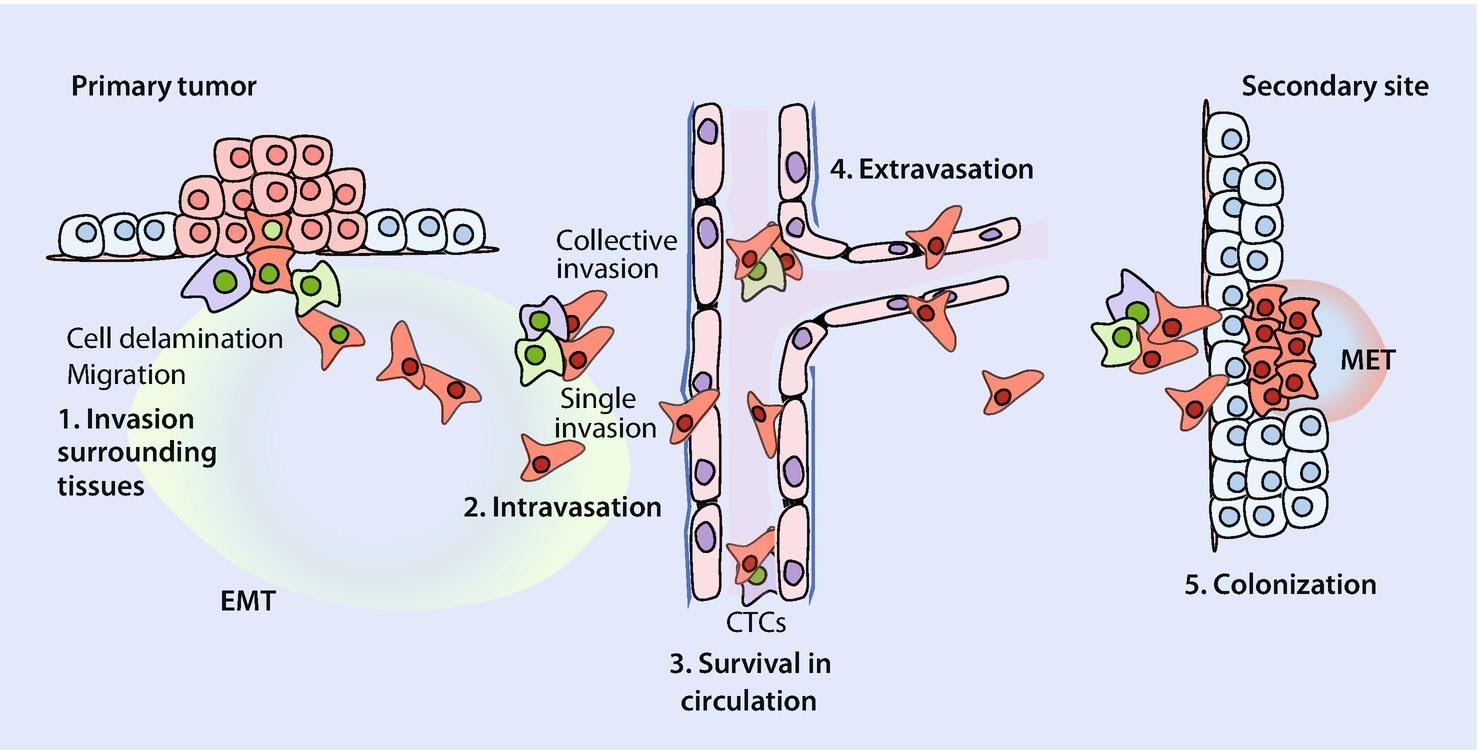
Through a literature survey, we were able to establish a network of genes and mRNAs that were responsible for driving phenotypic plasticity. The nodes of this network were the various molecular players and the edges were their interactions. A molecule could inhibit or activate the other molecules, which would decrease or increase their concentrations respectively, and certain molecules could inhibit or activate themselves.
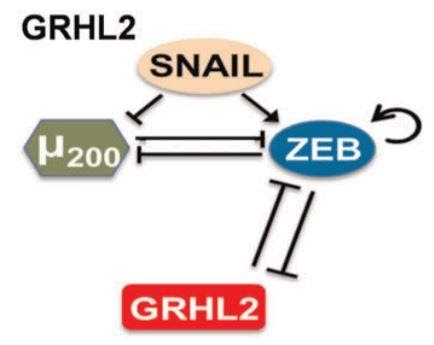
Let us look at a fundamental property that emerges from this network. We can see that μ200 and ZEB inhibit each other. Assume that ZEB is initially at a higher concentration than μ200. This would cause ZEB to have a stronger inhibition on μ200, reducing its levels. Now since μ200 levels are lowered, its inhibition of ZEB is consequently weakened. As a result of this weakened inhibition of ZEB, the levels of ZEB would increase further. This cycle repeats as the levels of ZEB are higher now, further weakening μ200. Thus, when the system stabilises, we would see a high level of ZEB and a low level of μ200. This interaction is what we call a positive feedback loop, where a slight disturbance can magnify itself and result in a much greater disturbance. Similarly, if the value of μ200 were higher initially, the system would result in a state of high μ200 and low ZEB. It is important to note that positive feedback loops can be much larger than this; the above example is just one of the types.
We used a computational model called RACIPE, which used the Hill Equation to describe the interactions between the various nodes of the network. After we input the nodes and their interactions into RACIPE, the model gives us an output of the various concentrations of these molecules. Using these concentrations, we can describe the type of cell that would be produced. Looking at our previous example and experimental evidence, we can classify the cells based on the outputs of ZEB and μ200.
High ZEB & Low μ200 ----> Mesenchymal
Low ZEB and High μ200 ---> Epithelial
Now that we can classify the two cell types based on the network’s output, we can study how the topology affects the emergent cells. For this, we modified our network to perturb the system and see how it responds. We can delete an interaction between nodes, change the type of interaction, add a new interaction, or delete a node. Some of these perturbations have biological analogues, such as the deletion of a gene, which would be called a knock-out in biological terms. The various perturbations can be thought of as mutations, and the original network would be the wild-type. After perturbing the system, we input the new topology into the model and see how it responds.
If a network gives rise to both cell types (mesenchymal and epithelial), that network would be plastic, since it allows the existence of both. In essence, this network would enable a cell to switch types. However, if a network gives rise to only one type of cell, this network is not plastic and would not enable the cells to change their phenotype. Our goal was to identify the properties that would make a network plastic, so we can prevent phenotypic plasticity and, in theory, prevent cancer from metastasising. We hypothesised that the number of positive feedback loops in a network is directly proportional to the plasticity of the network, as positive feedback loops tend to make it easier for disturbances in the system to change the trajectory (or) type of the cell.
The aforementioned perturbations would alter the number of positive feedback loops in the network, which gave us the chance to see if our hypothesis was correct.
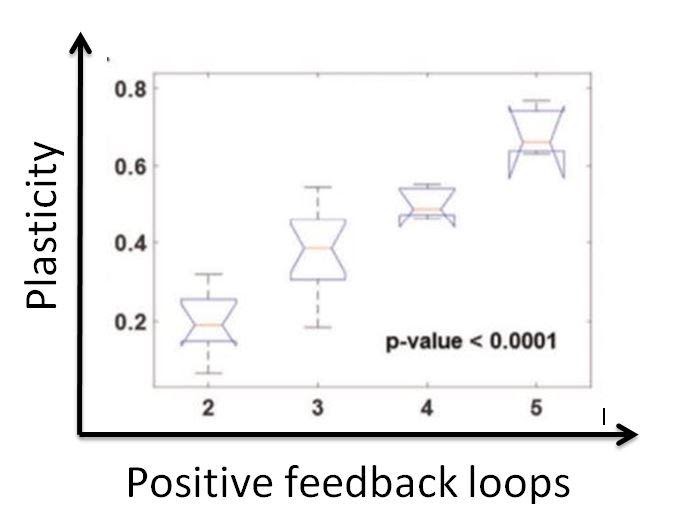
I still remember the sheer joy that consumed me when I arrived at this result. A clear and well-defined mathematical relation was unearthed in this analysis, and our hypothesis was spot on. The number of positive feedback loops does increase the plasticity of networks. Thus, through the magic of mathematical biology, we were able to identify an emergent property that drives phenotypic plasticity and consequently drives metastasis. If we are able to reduce the number of positive feedback loops, we would make the network non-plastic, and the cells would not be able to undergo a metamorphosis. Essentially, they are locked in their current state. If they are unable to undergo these changes, the cancer will no longer be able to spread, and therefore metastasis will be stopped. This is important as I had mentioned earlier that metastasis is responsible for 90% of cancer deaths. Our results aren’t of significance unless they can be experimentally verified. Fortunately, we do have experimental results that cement our hypothesis. A proposed therapeutic approach using our analysis would be to cut down the number of positive feedback loops by deleting nodes, or just interactions. The former is made possible with gene knockouts and the latter can be achieved by introducing a disturbance to the interactions by means of a drug or post-translational modifications.
If you would like to explore my research in greater detail, please refer to the paper I co-authored, published in Nature Partner Journals, Systems Biology and Applications.
Mathematical modelling in biology is gaining popularity within the research community for obvious reasons. I was always interested in biological systems, but I despise benchwork. The plague of contamination and failed Western blots never cease to scar my experiences in biological research. But in mathematical modelling, all of our experiments can be completed in a few lines of code, and we can get results in minutes, which would otherwise take weeks and months in a standard lab. We can invoke established mathematical results to delve deeper into the heart of living systems. Of course, conventional biological analysis will always be of importance, as mere modelling cannot be sufficient for establishing results. These results need to be confirmed with experimental evidence, and the construction of these models would be impossible without the vast data mines that experimental researchers have harvested. The way forward is a marriage between these two methods, where each method drives the other forward. Mathematical models can give us insights that will drive ideas for new experiments and establish results that would not have been possible otherwise. Experimentalists will continue to establish results with conventional methods and provide a strong basis for modellers.
After having had a taste of mathematical biology, I have taken an immense interest in the field. I am currently doing a remote computational neuroscience internship at the Theory of Neural Dynamics lab, Max Planck Institute for Brain Research, Frankfurt. As of now, my focus is on understanding the transportational dynamics of mRNAs and proteins along the axon of a neuron in terms of energy efficiency using a computational model.
If you would like to learn more about my research, please contact me at balaram.vishnu17@iisertvm.ac.in.


.svg)
.png)