Riemann Surfaces, as the name suggests, are certain types of surfaces. A surface is essentially something which locally looks “like” a flat plane. A natural example is the sphere, and we see this local flat plane structure everyday on the surface of Earth (flat-earthers will claim that in fact this structure is global). Another one is the doughnut (or the coffee mug for that matter), which is known as the Torus.
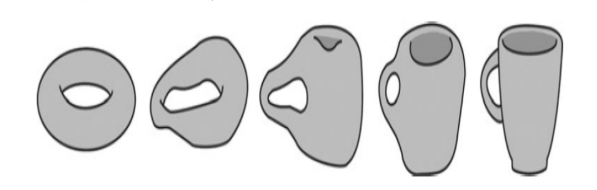
It turns out that every “nice” surface essentially is “determined” by the number of “holes” (known as the genus of the surface) it has. The sphere has zero, and the torus one.
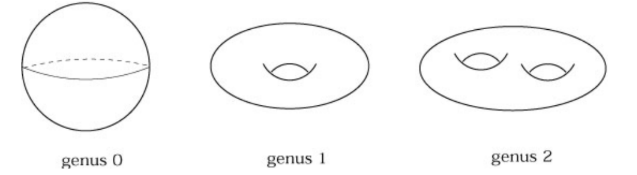
Now that we have some idea what surfaces are, let us get to understanding Riemann Surfaces. These are surfaces with some additional structure which helps in making sense of differentiability (technically speaking, holomorphicity/analyticity/complex differentiability) of a function on the surface.
This helps us in doing “calculus” (Complex Analysis of sorts) on the Surface. There can be many Riemann Surfaces with the same underlying “shape”. For example, there are many “non-equivalent” Riemann Surfaces whose underlying shape is the Torus. These are called Complex Tori. In fact, the set of all Complex Tori has a very nice Geometric structure, what is known as the moduli space of complex tori.
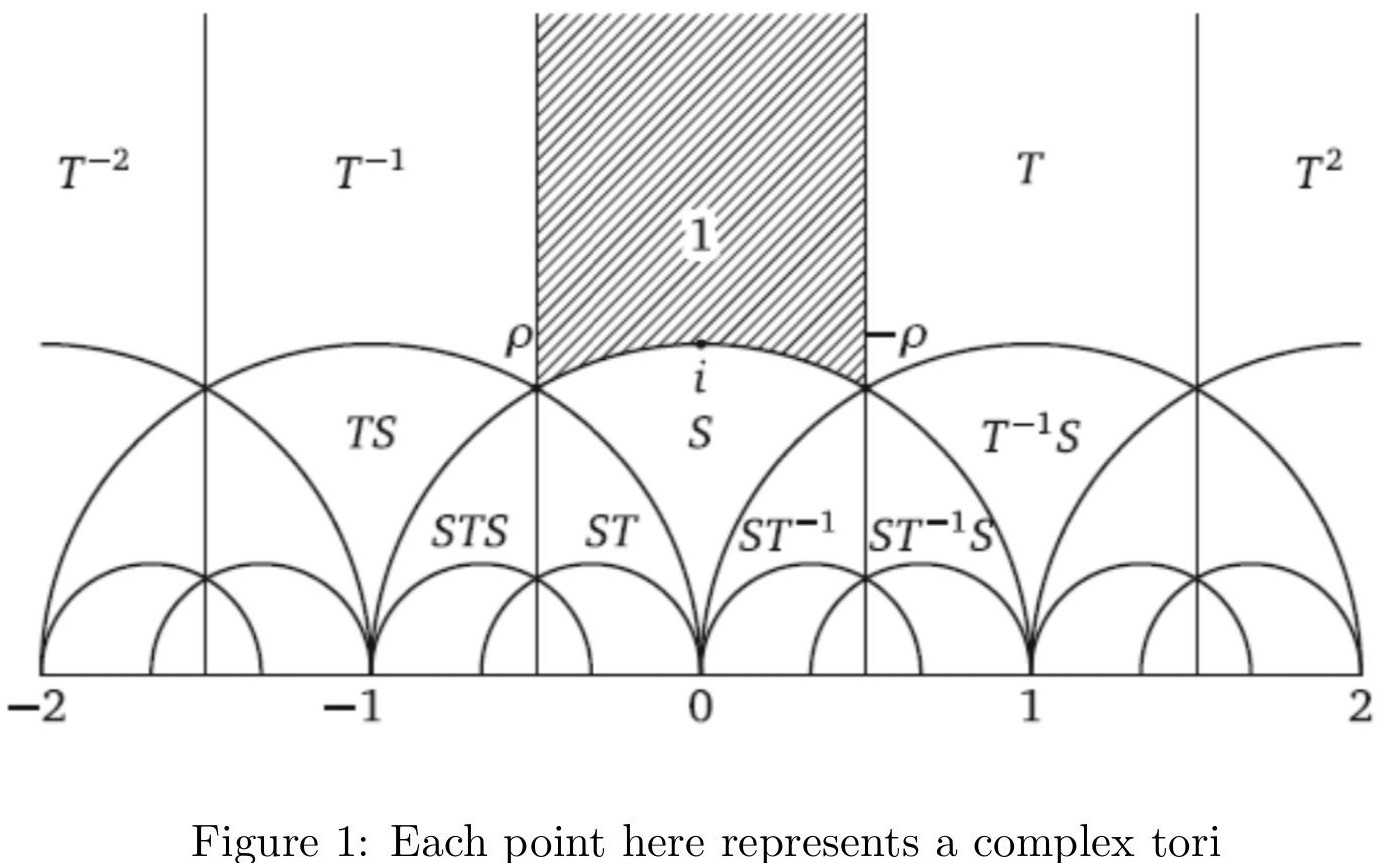
What is really fascinating is that the “shape” of the surface determines many things about the possible functions on the surface. For example, a very standard result known as the Hurwitz formula tells us something about any “nice” function between Riemann Surfaces in terms of their genera.
An area of mathematics deeply connected to the theory of Riemann Surfaces is Algebraic Geometry. The main objects of studies are the “solution”/zeroes of polynomials. One such object is the sphere, which is just the zero set of the polynomial
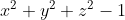
The essential idea is that a lot can be understood about the “Geometry” of the object by studying its algebraic description, and its algebraic properties (in terms of zeroes of polynomials). This has an intimate connection with Riemann Surfaces. In fact, it turns out that for all “nice” polynomials (of two complex variables), the zero set actually forms a Riemann Surface.
So, we see that the beauty of studying Riemann surfaces lies in the fact that the Geometric, Topological, Algebraic and Analytic structures of a Riemann Surface are interconnected, sometimes in obvious but sometimes in deep and subtle ways.


.svg)
.png)