Exact separation of radial and angular correlation energies in two-electron atoms

One of the biggest hurdles in quantum mechanics is finding solutions to the Schrödinger equation of many body systems. The truth is, the moment we step out of a two body system like the Hydrogen atom, the Schrödinger equation becomes much too complex to be handled analytically. Thus for the vast majority of chemical applications, the Schrödinger equation must be solved by approximate methods.The two primary approximation techniques used for this purpose are the variational method and perturbation theory. 

The basic idea of the variational method is to guess a “trial” wavefunction for the problem, which consists of some adjustable parameters called “variational parameters.” These parameters are adjusted until the energy of the trial wavefunction is minimized. The resulting trial wave-function and its corresponding energy are variational method approximations to the exact wave-function and energy. 

In the current study that we are going to look at, this method is implemented to solve the three body Schrödinger equation which applies for systems like helium and helium-like atoms(Li+, Be2+ etc) which is otherwise not exactly solvable. 

Now let us establish the coordinate system that we will follow.

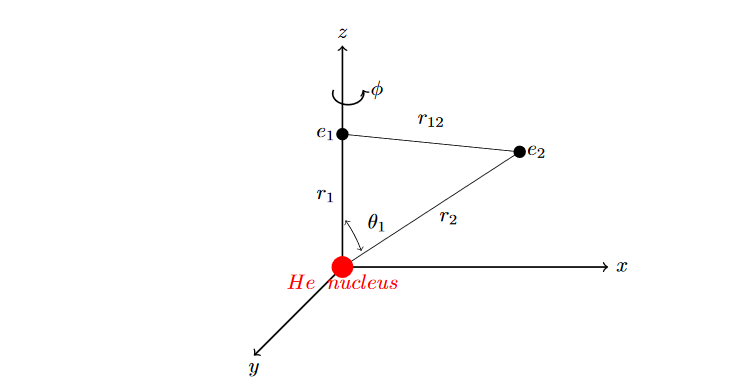
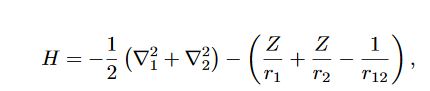
The terms in the above expression represent the kinetic energy of the first electron, the kinetic energy of the second electron, the electrostatic attraction between the nucleus and the first electron, the electrostatic attraction between the nucleus and the second electron, and the electrostatic repulsion between the two electrons, respectively. 

In the late 1920’s, different variational trial functions were proposed to improve the results obtained for the ground state energy of He(E0 = -2.90372 hatrees). 

wavefunction parameters energy (in hatrees) 

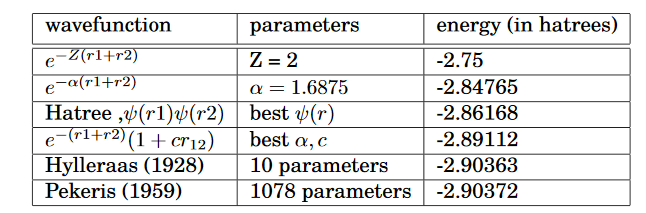
 If we look at the third entry in the table, we can clearly see that even the best choice of one- electron wavefunction ψ(r) results in considerable error in the E0 value. This error is to the negligence of variable r12 in the function. The effect is known as electron correlation. On inclusion of this r12 into the wavefunction, we can see considerable improvement in the values. In 1928, Egil Hylleraas proposed a variational formalism; 

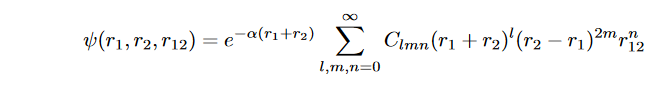
where l, m, n ∈ Z. The convergence of this trial function is studied by progressively increasing the number of basis functions. This wavefunction explicitly accounts for correlation between two electrons and obtained the nearly exact result with 10 optimized parameters. Now for the purpose of this study, if we say that 

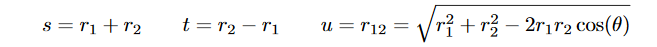
Then the Hylleraas function becomes 

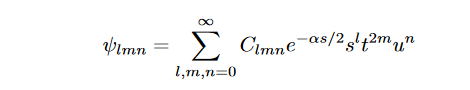
In order to solve the Schrödinger equation, the Laplacian also needs to be translated to the Hylleraas coordinates. For the Hylleraas wavefunction, the Kinetic energy Hamiltonian is;

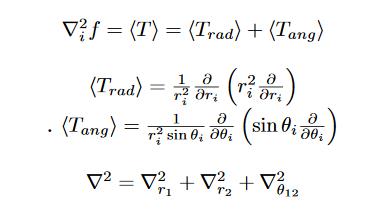
Replacing the r1, r2 and r12 with s, t and u gives us the Laplacian in Hylleraas coordinates. Subsequently, the integral, <ψ| − (∇/2)^2|ψ> is setup. The advantage is that these resulting integrals after the conversion have a standard result(Primitive integral) or in other words, they are analytically solvable.

The main subject of interest in this study is how the Hylleraas representation simplifies the estimation of electronic correlation. 

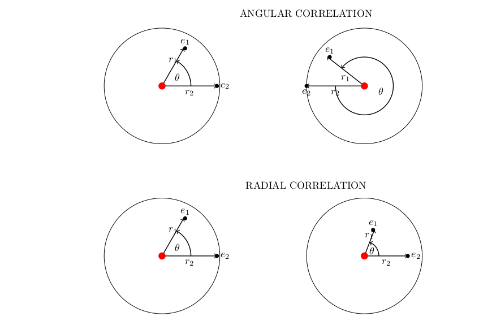
Correlation energy is a measure of how much the movement of one electron is influenced by the presence of all other electrons. It arises from the correlated part of the two-particle wavefunction, i.e., part of the wavefunction which cannot be expressed as a product of two one-particle wavefunctions.

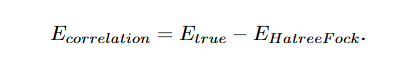
This correlation can be interpreted as correlation in radial and angular motions of two electrons. With this approach the exact separation of angular kinetic energy from the total energy is achieved. This angular kinetic energy is equal to the angular correlation energy(Eang c ) because it arises from the coupled r12 term. Also; Erad c = Ec - Eang c . 

This enables better understanding of the contributions of angular and radial correlations to the stability of the atom. This new method challenges the conventional method of radial and angular correlation energy calculations by pointing out a discrepancy in the numbers. This discrepancy is introduced as a new radial-angular coupling term which was previously unknown and was as- sociated with angular correlation. As an after effect, the radial correlation which was previously thought to contribute less to the total correlation is corrected to 60% of total correlation in He atom. This a fundamental quantum mechanics study that proposes a new and easier method to compute the energies of two-electron systems. A lot of the math that is involved is chucked for simplicity but if you are interested do read the cited publication[1]. 

Richard Feymann once said ”I think I can safely say that nobody understands quantum mechanics”. It is so true. The more we think we understand the subject the farther we drift. As young researchers all we can do is to strive to get profoundly shocked and amazed every time it tells us a new secret. But out of all the possibilities that may arise when you roll a dice with infinite faces, some struck right. Ergo...the universe exists. 

Reference :

[1] A. Kammath and R. Ramakrishnan. Exact separation of radial and angular correlation energies 

in two-electron atoms. Chemical Physics Letters, 720, 2018.